under construction
Последний раз обновлено 27.06.01
Для учебных целей за эту задачу, может быть, стоит браться только тем, для кого она, ее предметная область, понятна. Будем считать, что мы знаем, зачем измерять сигналы, а вот писать программы умеем хуже. Я уже говорил, что для ООП задача должна быть сформулирована до начала программирования, поэтому попробуем сделать это. С другой стотроны, возможно формулировка задачи поможет даже тем, для кого предметная область не столь понятна. Сокращения: мс(m) милли, мкс(mk) микро, ПФ,ДПФ,БПФ - преобразование Фурье,дискретное и быстрое.
Постановка задачи для программы OSC
Процесс отображения состояния устройства сбора данных на параллельном порту можно просто считать отображением сигнала, значение амплитуды которого в заданные моменты времени мы, может быть в другие моменты времени, считываем с этого порта.
Отображение сигнала вообще можно разделить на две подзадачи:
К обоим пунктам, если мы не хотим получить игрушечный, просто красиво отображающий линии девайс, можно применить следующее требование: не потерять ничего, все всплески реального сигнала должны быть зафиксированны. На это влияет и стабильность выборки, улучшить которую можно существенно лишь аппаратно.
В задачу осциллографа не входит измерение параметров сигнала численно. Достаточно лишь отобразить его форму, чтобы существенные качественные параметры были сохранены.
В качестве прототипа можно рассматривать любой существующий осциллограф, например старый бытовой С1-94, предоставляемого им сервиса достаточно для многих применений.
Постановка задачи для программы OSC
Я уже не хочу писать программы с сегментами по 64К и сидеть в памяти до 640К. Это все требует процессора не ниже 386. Сама по себе задача обработки сигнала несколько специфична: нужно только уметь быстро умножать, складывать, пересылать данные и делать это стабильно во времени. Процессор общего назначения, такой как 386, плохо приспособлен для этого, не поддерживается это и архитектурой самого PC, поэтому при общих больших вычислительных возможностях и высокой тактовой частоте того же 386 не удается легко их для этого использовать. В любом случае, лучше пожертвовать рекордными параметрами для повышения качества отображения.
Мы можем пойти путем выноса всех операций реального времени за рамки PC во внешнее устройство, а можем минимизировать внешнее устройство совсем до предела, максимально используя аппаратуру компьютера. Все эти отличия должны войти в драйвер - источник данных для остальных объектов программы. Здесь мы будем рассматривать драйвер для минимальной внешней аппаратуры.
Постановка задачи для программы OSC
Такой драйвер должен будет тактироваться от внутренних часов компьютера, выбирая данные из порта через некоторое число тактов. Нужна однозадачная однопользовательская операционная система реального времени. Я не знаю ничего, что бы подошло для этого лучше ДОСа и любого экстендера, который даст flat модель памяти. Ворочать файлами и ДОС сервисом из под экстендера во время отображения нам не требуется, поэтому их роль во время отображения просто сведется к тому, что программа будет выполняться в защищенном режиме, но все равно, для написания такого драйвера придется:
Как ни крути, для сложного внешнего устройства, если и не пришлось бы изучать вообще другой процессор и иметь возможности для его программирования, то пришлось бы создавать сложную схему, а в нашем случае будет достаточно подключить что то вроде АЦП к порту по любой схеме, с чем справиться легче.
Но не так все страшно, как может показаться на первый взгляд. Дело в том, что учитывая особенности системы прерываний, работы с портами и то, что стандартный АТ таймер тактируется с частотой 1 МГц, если особенно не мучиться, то быстрее чем раз в 10 мкс стабильно снимать данные с порта не получится, а на таких скоростях мало какие особенности аппаратуры могут серьезно мешать.
В этом случае, драйвер будет формировать блок данных для отображения, прерывая программу отображения по прерыванию таймера, при внешнем устройстве этот блок для отображения просто можно было бы считать, например, блочным вводом. При выключенном отображении этого не происходит и можно спокойно использовать все функции экстендера и ДОС по работе с памятью, файлами и прочее.
Постановка задачи для программы OSC
Непрерывный во времени сигнал мы отображаем в ограниченном по размеру окне. По достижении правого края окна луч реального осциллографа завернет на начало и продолжит отображение. Рассмотреть таким образом можно только периодические сигналы, период которых согласован с границами экрана. Для них при любой частоте повторной прорисовки кадра луч попадет на одну и ту же линию.
Непериодические или несогласованные периодические сигналы в зависимости от соотношения их формы, частоты и частоты повторения прорисовки окна дадут разные эффекты на экране и невозможность работать с сигналами.
Для отображения изменяющихся изображений можно использовать технику двойного буфера, например: две видеостраницы и переключение их во время обратного хода кадровой развертки монитора. Обратный ход происходит с фиксированной частотой. Скорость рисования в видеобуфере определяется параметрами Т/дел и количеством делений.
Нужно не допустить, чтобы части сигнала попадающие в разные видеобуферы отображались разное количество раз в секунду, если рассматривать схему отображения: ждать развертку - очистить - обновить из следующего видеобуфера. Эти части сигнала будут отображаться c разной интенсивностью, а это лишняя помеха, которая помешает работе с сигналом и исказит его.
Постановка задачи для программы OSC
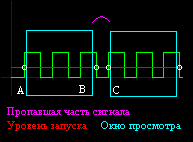
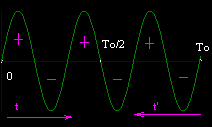
Пока рассмотрим периодический сигнал. Уровень запуска работает как один из способов синхронизации фазы, начала периода сигнала с границами экрана. Рисунок (Рисунок 1.5) показывает расположение сигнала в окне, или окон на сигнале, за два периода. Красной линиией обозначен уровень запуска. Точки A,B,C на сигнале совпадают с этим значением. Ясно, что точка B не может быть использована, т.е. запуск нельзя сделать только сравнивая со значением сигнала, надо учитывать и направление изменения сигнала.
Такой способ сстабилизации фазы при запуске, как задание времени, периода исследуемого сигнала не позволит, на практике, зафиксировать изображение на экране из-за погрешностей измерения времени и нестабильности сигнала. Нужная фаза сигнала будет ползать по экрану влево-вправо, что при определенных соотношениях скорости ползанья и периодов приведет, например, к сплошной заливке или другим помехам, которые не дадут рассмотреть сигнал.
Рисунок 1.5
Расположение сигнала в окне

Постановка задачи для программы OSC
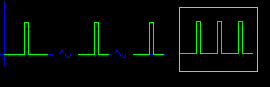
Есть большое число специальных случаев, когда организовать работу с сигналами обычным образом нельзя. Вот ряд примеров:
Рисунок 1.6
Вариант специального отображения
Постановка задачи для программы OSC
Вот список основных параметров, которые интересуют нас как программистов, часть из них изменяется пользователем, часть характеризует его возможности. Я не буду их подробно описывать, просто перечислю. О сервисе для упрощения работы с осциллографом типа: установка меток, тестовые сигналы и прочее мы пока говорить не будем.
Перейдем к тому, что делать с сигналом: как его оцифровать и отображать. Все слышали что сигнал должен быть оцифрован с частотой дискретизации Fд>2*Fгр, где Fгр - наивысшая гармоническая составляющая в спектре сигнала. В этом случае, сигнал может быть восстановлен без ошибок.
Попробуем понять, откуда это берется. Опять применим объяснение, имеющее физический смысл для тех сигналов, с которыми мы имеем дело. Многие почему то останавливаются на этом шаге, попробуем облегчить его прохождение.
Часть 16 цветных картинок я сжал как JPG. У меня, неожиданно, не нашлось декодера для GIF, а тот который есть, кодирует так, что кроме него никто этот формат не опознает. Кого не устраивает жуткое качество моего декодера JPG, могут скачать архив из PCX здесь скачать(download).
Пусть есть сигнал, который можно представить в виде
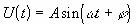 (1)
(1)
где A Вольт - амплитуда, 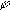
t сек -время, 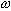 =2*
=2*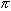 *f
*ff Гц -частота.
Мы можем нарисовать такой сигнал, если будем знать все три параметра: A,, которые нам надо извлечь из входного сигнала. В принципе, амплитуду, в данном случае, мы можем получить пиковым детектором, зная амплитуду, в момент 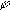 ,
,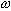
t=0 можно найти фазу, измерив U(t). Как определить частоту 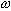
U(t), которое даст нам 1, если частота U(t) совпадет с частотой тестового, опорного сигнала и 0 в остальных случаях.
Видимо, существует много способов сделать это. Одним из способов является использование факта гармоничности сигнала.
Рассмотрим гармоническую функцию sin( или 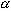 *t)
*t)cos( с циклической частотой 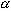 *t)
*t)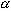
Tсобств=2* сек.
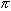 /
/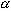
Легко видеть, что площадь фигуры под графиком такой функции, интеграл от sin( или 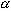 *t)
*t)cos( по 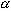 *t)
*t)dt (по времени) за период интегрирования Ti=Tсобств*n сек, где n -целое, равен нулю.
Поэтому интеграл от гармонической функции, которая укладывается в период интегрирования Ti целым числом n собственных периодов Tсобств равен нулю (*).
Будем сравнивать сигналы sin( и 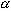 *t)
*t)sin( с периодами 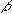 *t)
*t)Tсобств=2* сек и 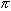 /
/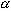
Tсобств=2* сек.
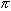 /
/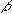
Интеграл от произведения сравниваемых сигналов sin( по 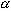 *t)*sin(
*t)*sin(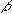 *t)
*t)dt (по времени) за период интегрирования Ti=Tсобств*n сек, при 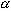 =
= 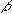
Ti/2.
Рассмотрим интеграл от произведения сравниваемых сигналов sin( по 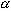 *t)*sin(
*t)*sin(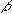 *t)
*t)dt (по времени) за период интегрирования Ti сек, при 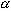 !=
!= 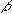
( и разностной 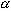 +
+ 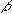 радиан/сек)
радиан/сек)( частот. Это легко написать на бумажке, но затруднительно здесь, в текстовом режиме.
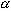 -
- 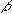 радиан/сек)
радиан/сек)
Мы хотим найти такие 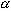 ,
,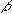 ,Ti
,Ti(*), это может произойти, если суммарная и разностная гармонические функции будут укладываться в период интегрирования Ti целым числом своих периодов Tсобств.
Рассмотрим ряд частот синусов, каждая из которых в целое число раз k больше минимальной частоты f=fo, Гц:
f, 2f, 3f, ... , Nf, ... , Mf, здесь M=2*N (2)
Этим частотам соответствуют периоды, сек:
T, T/2, T/3, ... , T/N, ... , T/M
Нам надо найти такой период интегрирования Ti, чтобы любая суммарная или разностная частота для двух сравниваемых из (2) попала бы в Тi целым числом периодов. Возьмем период Тo=Т от самой меньшей частоты fo из (2). Любая k-я частота из (2) попадет в этот период То ровно k периодами. Суммарная и разностная(абсолютное значение) частоты для любых kf из (2), таких что k<=N, попадут в этот же ряд (2).
Ясно, что период То не будет наименьшим для любых двух сравниваемых из ряда (2), но он будет подходящим для всех частот из ряда (2) в том смысле, что интеграл от произведения не совпадающих по частоте синусоид из (2) за период интегрирования Тi=То будет равен 0, а от совпадающих То/2. Если мы разделим наш тестовый интеграл на To/2, то получим настоящий компаратор, который выдаст 1, если сравниваемые частоты совпали и 0 в противном случае.
Итого, для функции вида (1) с единичной амплитудой и нулевой начальной фазой получим:
*sin(k*fo*t))](img8/u1.jpg) , Am=1, если m=k
, Am=1, если m=k
Если в (1) вместо синуса стоит косинус, то изложенное выше годится и здесь, взяв в качестве тестовой функции косинус.
*cos(k*fo*t))](img8/u2.jpg) , Bm=1, если m=k
, Bm=1, если m=k
Если входной сигнал имеет вид
(1)+Uo=
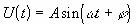 +Uo (1.1)
+Uo (1.1)
т.е. есть постоянная составляющая, то проинтегрировав (1.1) по периоду Ti, и разделив результат на Ti, получим Uо.
+Uo)](img8/u3.jpg)
Вернемся к вопросу, который был задан ранее: определить частоту 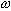
[fmin,fгр] Гц входного сигнала, задать шаг приращения частоты для N частот из ряда (2), которые будут тестовыми функциями и с которыми мы будем сравнивать и перебрать их до нахождения не нулевого интеграла от произведения. Это и будет искомая частота.
Что это за шаг для приращения частоты? Если наш диапазон [1,100] Гц, то это не означает, что можно обнаружить только любую из ряда
1, 2, ... , 100 Гц
Мы не можем изменять k - это целое число, поэтому нам остается только изменять fo из ряда (2). Выбор fo полностью определяется тем, с какой точностью вы собираетесь различать составляющие во входном сигнале.
Легко заметить, что чем меньше этот шаг, тем больший по времени период интегрирования Ti нужно взять, чтобы частоты, отличающиеся только на fo попали в него целым числом периодов. Можно даже бездоказательно предположить, что при fo -> 0, Ti -> бесконечности и получается что-то вроде несобственного интеграла.
Диапазон сравнения частот зависит от [fmin,fгр], сравнение начинается с fmin, а заканчивается с fгр.
Внесем небольшую поправку. Мы считали в наших рассуждениях, что оба сравниваемых сигнала имеют единичную амплитуду. Если предположить, что только тестовый сигнал имеет единичную амплитуду, то на выходе компаратора мы получим вместо 1 амплитуду сравниваемого сигнала, если он совпал по частоте с тестовым сигналом и ноль в противном случае. Можно смело отказаться от пикового детектора.
Пусть теперь, что чаще всего и бывает, мы не можем начать измерение (1) синфазно, т.е. начальная фаза 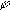
Найдем синусоидальную составляющую такого сигнала.
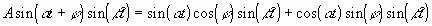 (*)
(*)
cos(
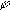 )=const, sin(
)=const, sin(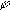 )=const
)=const
Проинтегрируем эту сумму (*), константы вынесем за интеграл. Появился новый интеграл cos(, который равен нулю на 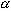 *t)*sin(
*t)*sin(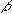 *t)
*t)Ti для любых 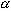 ,
,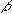
После интегрирования, вместо амплитуды синусоидальной составляющей, имеем Am=A*cos(. Одно уравнение и два неизвестных, надо еще какое-то условие.
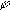 )
)
Аналогично найдем косинусоидальную составляющую такого сигнала, получим Bm=B*sin(. В данном случае, за 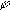 )
)B я обозначил традиционно амплитуду для косинусоидальной составляющей, а для этого сигнала вида (1) B=A. Имеем два уравнения и два неизвестных. Можно решить разными способами, в зависимости от условий вычислений, например так:
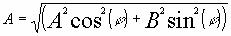 ,
,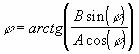
Для входного сигнала вида (1), частота которого принадлежит некоторому ряду (2) и лежит в диапазоне [fmin=n*fo,fгр=m*fo] (*) Гц, fo Гц - шаг, точность, мелкость разбиения входного частотного интервала, можно узнать его параметры A, путем сравнения с тестовыми функциями вида 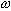 ,
,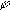
sin(2* и 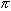 *k*fo*t)
*k*fo*t)cos(2* с частотами из ряда (2) и интервала (*), перебирая частоту тестового сигнала по всему диапазону до нахождения не нулевого интеграла от произведения тестовой функции и сигнала, интегрируя на периоде частоты 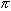 *k*fo*t)
*k*fo*t)fo.
Принцип детектирования, обнуления интеграла на не совпадающей частоте тестовой функции и сигнала, основан на подборе периода интегрирования, такого что суммарная и разностная частоты (эквивалентные перемножению тестовой функции и сигнала) при не совпадающих частотах при интегрировании на нем дают ноль.
Сигнал вида (1) можно представить как сумму двух сигналов sin и cos с одинаковой частотой, нулевой фазой и зависящими от фазы (1) амплитудами. В обратную сторону тоже верно.
Пусть входной сигнал состоит из нескольких независимых сигналов вида (1), в диапазоне частот [fmin,fгр], каждый из них принадлежит ряду (2), т.е.
](img8/u6.jpg) ,
, 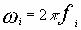 ,
, 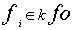 ,
, 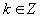
В этом случае, при сравнении с каждой тестовой функцией из ряда (2), составляющие входного сигнала не мешают друг другу при детектировании.
Для сложного входного сигнала можно нарисовать на графике по оси ординат амплитуды всех составляющих, а по оси абсцисс отложить либо номера гармоник из ряда (2), либо абсолютные значения частот. Такая зависимость называется амплитудным спектром сигнала. То же самое можно сделать для фазы и получить фазовый спектр.
Полезность такого спектра, например, для фильтра очевидна, получив спектр входного сигнала, можно избирательно и произвольно исключить некоторые составляющие и опять сгенерировать сигнал по его параметрам.
Ранее мы требовали, что в спектр входного сигнала входят только частоты из ряда (2). А что будет, если в этом сигнале окажутся еше и составляющие в промежутках между значениями k*fo?
Все зануления интегралов для не совпадающих частот касались только частот из ряда k*fo. Те гармоники, которые не уложаться целым числом своих периодов на период интегрирования дадут некоторое значение после интегрирования с любой тестовой функцией k*fo из (2), в общем случае не равное нулю, хотя в сигнале нет такой частоты k*fo. Рисунок (Рисунок 2.17.1) показывает простой пример такого случая.
Рисунок 2.17.1
Не кратные Ti и fo частоты
На графике можно заметить, что приближая частоту к попаданию целым числом периодов на период интегрирования, т.е. приближая ее к какой-то fi из ряда (2) амплитуда от интегрирования с тестовой функцией fi будет приближаться к правильной, и при совпадении с fi пропадет влияние этой составляющей на другие из ряда (2).
Мы не можем рассчитывать на то, что не попавшая в ряд k*fo составляющая входного сигнала будет влиять только на частоты ряда (2), которые оказались рядом со значением частоты этой составляющей. Такая составляющая ошибочно отметится при сравнении со всеми частотами из (2) в виде ложной амплитуды, амплитуды составляющей которой нет во входном сигнале. Значение этой ложной амплитуды будет зависеть от соотношения частоты помехи и частоты тестовой функции.
Мы не будем пока выяснять закон, по которому распределена помеха, будем пока считать что эта возможная ложная амплитуда достаточно мала и лежит ниже некоторого порога.
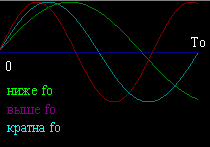
Такое влияние дискретности не бесконечно малого, конечного шага приращения частоты, или, что равнозначно, конечного во времени периода интегрирования Ti приводит к тому, что получается спектр, например, амплитудный, который состоит как бы из "областей", а не из "палочек", т.е. преобразованием мы снимаем сумму от амплитуд составляющих умноженных на некоторые коэффициенты (вероятно меньшие единицы) в некоторой области, а не только точно от составляющей k*fo, сама k*fo умножается на единичный коэффициент. Рисунок (Рисунок 2.17.2) качественно это демонстрирует.
Рисунок 2.17.2
Преобразованием мы снимаем сумму от влияний составляющих в некоторой области, а не в точке k*fo
Это говорит так же о том, что мы не можем различить во входном спектре частоты, отличающиеся менее чем на fo. Очевидный метод борьбы - увеличение периода интегрирования Ti и, соответственно, уменьшение fo.
Получение параметров A, от составляющих входного сигнала с помощью интегрирования с тестовыми функциями называют преобразованием Фурье, но как бы его не называли, это преобразование можно использовать для этих целей.
 ,
,
Получить исходный сигнал U(t), зная параметры его составляющих, можно просто сложением значений этих составляющих в каждый момент времени, это называют обратным преобразованием Фурье.
Любой может открыть книгу по основам мат. анализа и более точно узнать о преобразовании Фурье и требованиях к сигналам и вычислениям.
Нам на практике надо численно, а не аналитически рассчитывать интегралы для преобразования Фурье. U(t) будет поступать к нам с АЦП, как часто надо считывать с него значения и что с ними делать? Введем следующие определения.
[fmin,fmax]
fо, ГцМfо и  . M=
. M= /fo
/foТпре, секTi, определяется так же из шага, мелкости разбиения частотных спектров входного сигнала fo.
fд, ГцU(t) из АЦП.
Тд, секfд
NТд уложится за Тпре и определяется как N=Tпре/Тд
Нам надо отыскать подходящую fд для заданных условий. Опять рассмотрим сигнал вида (1). Если посмотреть на график sin, то будет видно, что выбирая значения через некоторый Тд по времени, мы непрерывную линию заменяем набором точек. Наша задача сводится к тому, чтобы найти некоторое количество точек на оси времени, при которых интеграл в преобразовании Фурье, как предел сумм, может быть для наших целей безболезненно заменен на конечную сумму из значений U(t) в этих точках.
k*fo должна при суммировании в этих точках дать ноль;
Тогда можно будет заменить интегрирование на суммирование.
Предположим, что искомая частота дискретизации тоже принадлежит ряду k*fo.
Дискретное преобразование Фурье (ДПФ)
Рассмотрим пока вариант, при котором только синусоидальные составляющие входят в состав входного сигнала. Любая частота из (2) попадает целым числом k периодов на Tпре. Мы можем подобрать правило для попарного выбора точек t из интервала Тпре так, что каждое суммирование значений функции в этих точках даст ноль и любая точка войдет в каждую пару только один раз, например такое, рисунок (Рисунок 2.21):
Рисунок 2.21
Правило для попарного выбора точек
sin(2*
 *k*t) и sin(t’)=sin(2*
*k*t) и sin(t’)=sin(2* *k*(Tпре-t)) (6)
*k*(Tпре-t)) (6)
То, что fд принадлежит (2) означает, что она тоже попадет в Тпре целым числом периодов Тд, т.е. первый и последний периоды, и далее попарно равноотстоят от краев интервала Тi, или последовательность точек {Тд*n} симметрична относительно центра Тi/2. Можно подставить в (6) вместо t=Тд и мы увидим, что при выборке с частотой дискретизации fд, которая принадлежит (2) синусоидальные составляющие из тогоже ряда (2) при суммировании в этих точках занулятся. Первое требование для замены интеграла на сумму мы выполнили.
Синусоидальная составляющая попадает в Тпре/2 нулем, поэтому можно взять ровно N точек в интервале [0,Тпре-Тд] с шагом Тд, заменив t=Тпре на t=Тпре/2.
|
Дискретное преобразование Фурье (ДПФ)
Для заданного диапазона частот [fmin,fmax] с шагом fо
[2*fmin, 2*fmax]
[fo,fmax-fmin] (отбросим частоту ноль - постоянную составляющую)
Таким образом, самый широкий диапазон составляющих, которые должны обнуляться при суммировании их значений в точках t=Тд*n на Тпре будет [fo,2*fmax].
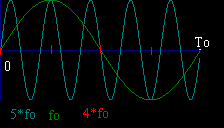
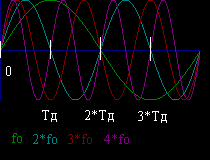
Рассмотрим рисунок (Рисунок 2.22.1). Суммируем по N=4 точкам произведение единичной синусоидальной функции с частотой fд=4*fo (Тд=Тпре/4). Неотличимы составляющие 5*fo и fo.
Рисунок 2.22.1
Частоты fo и 5fo
Еще пример, рисунок (Рисунок 2.22.2). Суммируем по N=4 точкам произведение единичной синусоидальной функции с частотой fд=4*fo - самая высокая составляющая во входном сигнале. Из рисунка видно, что для частоты
4*fo можно получить только нули
2*fo то же самое
fo амплитуду умноженную на N/2
3*fo неотличима от fo с точностью до знака
Рисунок 2.22.2
Частоты fo, 2fo, 3fo и 4fo
Дискретное преобразование Фурье (ДПФ)
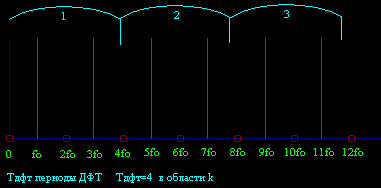
Если рассмотреть другие составляющие k*fo, б"ольшие предыдущего fд, т.е. k>4, то можно заметить,что некоторые составляющие будут давать свои амплитуды так же как их дают составляющие в рассмотренном выше примере. Т.е. ДПФ оказалось, в отличие от простого преобразования, периодичным в области номеров k, или абсолютных значений частот k*fo Гц на частотных спектрах. Период ДПФ в области номеров k: Тдпф=fд/fo. Для этого примера Тдпф=4, рисунок (Рисунок 2.23.1).
Рисунок 2.23.1
Период ДПФ в области номеров k. Для этого примера Тдпф=4
Периодичность означает, что для любой частоты k, значение амплитуды совпадет с частотой k+Тдпф*n (*) , т.е. эти частоты будут неотличимы, и если все эти частоты из (*) присутствуют в спектре с разными амплитудами, то на данном наборе точек {Тд*n} будут получены равные для всех них значения, зависящие от соотношения амплитуд и, в общем случае, не являющиеся амплитудами ни для одной из этих составляющих.
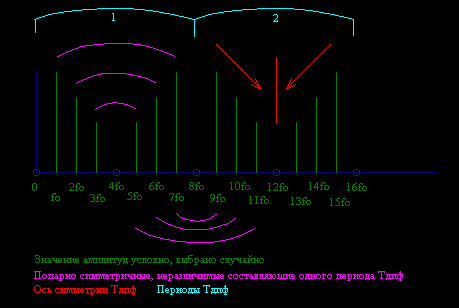
Если увеличить k для fд, то можно заметить, что внутри периода Тдпф отличимы, независимы только половина частот, т.е. fo и 3*fo отличаются только знаком, и, например, если обе эти частоты будут в сигнале и иметь одинаковую амплитуду, то на данном наборе точек {Тд*n} мы получим, что их амплитуды нулевые. Составляющие внутри периода Тдпф зависимы симметрично относительно середины периода ДПФ Tдпф/2, рисунок (Рисунок 2.23.2).
Рисунок 2.23.2
Структура спектра ДПФ
fдДискретное преобразование Фурье (ДПФ)
Экспериментально, без доказательства, можно заметить, что для получения независимых линий в спектре с помощью ДПФ используется половина периода Тдпф, это диапазон [fo;fд/2-fo], либо одна из попарно зависимых частот всего периода. Частоте k=0 соответствует постоянная составляющая.
Можно провести подобные эксперименты и с косинусоидальными составляющими, что позволит нам предположить, что выбор частоты дискретизации происходит по такому условию
fд >= 2*(fmax+fo)
Строгое математическое доказательство и подробные ограничения на сигнал даются в теореме Котельникова, который в определенных кругах известен как Найквист.
fдДискретное преобразование Фурье (ДПФ)
Рассмотрим пример: дана полоса одного сигнала [1;1,1] МГц, второго сигнала [100;200] КГц. В обоих случаях fo=100 КГц. По достаточному условию в первом случае fд=2*(1,1+0,1)=2.4 МГц, во втором fд=2*(200+100)=600 КГц. С точки зрения вычислительных и аппаратных затрат разница существенная.
Если немного самостоятельно порисовать эти Тдпф, то может показаться, что fд должна зависеть в основном от количества независимых частот в спектре, от М и 
fmax, другими словами, нам удобно снизить fд и проводить преобразование для сигнала в первом периоде Тдпф. Это эквивалентно уменьшению числа необходимых точек на сигнале, полученных из достаточного условия.
Поиск имеет смысл, когда ширина полосы 
fmin и fmax, т.е. для полосы аудиосигнала [0,02;22] КГц ничего искать не нужно, используется достаточное условие.
Разумеется, чем больше точек мы возьмем, тем устойчивей мы будем к случайным помехам в сигнале, в идеале нам надо взять все точки сигнала, но во многих случаях сигнал является стационарным за время интегрирования, преобразования, а снижение частоты дискретизации просто делает возможными всякие замеры. Мы будем считать сигнал подходящим для такого снижения fд.
Для начала, нам необходимо убрать все сигналы за пределами нашей полосы [fmin;fmax] до использования ДПФ в любом случае.
Если наша полоса не непрерывна, то можно попытаться утрамбовать ее в первый Тдпф в обе половины, следя, чтобы не получалось попаданий в зависимые частоты. Но в общем случае можно указать более простой алгоритм, который дает меньшую паковку но все же снижает fд.
Рассмотрим пример: полоса [5;6] Гц, если fо=1 Гц, то М=2 - число независимых частот, 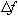 =2
=2fд=2*( Гц, то в первом периоде будут независимые частоты 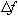 +fo)=2*(2+1)=6
+fo)=2*(2+1)=6{1,2,4,5} Гц, это можно увидеть нарисовав первый период амплитудного спектра для fд=6 Гц. Мы выбрали fд неудачно, наша частота входного сигнала 6 Гц не попала в различимые ни в одной из половинок. Надо брать fд=8 Гц, первые две частоты 5,6 Гц во второй половине Тдпф будут нам нужны, а частота 7 Гц не будет использоваться.
Как это определить для произвольных параметров? Надо, чтобы соответствующие реальному диапазону входного сигнала частоты в первом Тдпф были все либо в левой половине, либо в правой и не заезжали на границы fд*n/2, тогда все нужные частоты будут различимы (**). Это утверждение наводит на мысль, что искомая частота fд будет лежать где-то тут: 2*(.
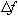 +fo) <= fд <= 2*(fmax+fo)
+fo) <= fд <= 2*(fmax+fo)
fд для первого ТдпфДискретное преобразование Фурье (ДПФ)
Обозначим за m частоту из первого полупериода Тдпф [1;fд/(2*fо)). Это ряд частот {m*fo+fд*n}, n - номер Тдпф.
Обозначим за m2 частоту из второго полупериода Тдпф (fд/(2*fо);fд/fo). Это ряд частот {m2*fo+fд*n}, n - номер Тдпф.
Зададим, что k*fo != fд*n/2, n=1,2,3.
fд=2*(М+1), М - число гармоник
fд смотри в исходнике, увеличиваем fд до выполнения условий (**).
Тдпф n={fmin или fmax}/fд
n-м периоде Тдпф. Если {fmax или fmin} < n*fд+fд/2, то первая половина.
Тдпф следует, что k*f=k*f+fд*n, т.е. расположение в n-м периоде Тдпф нужной полосы частот соответствует расположению в первом (при n=0) периоде Тдпф. Номер k" в первом периоде Тдпф для k*f из n-го периода определяется как k"=(k*f-fд*n)/fo.
Можно скачать архив с исходником и откомпилированной программой здесь скачать(download), которая пытается понизить частоту fд, по сравнению с получаемой из достаточного условия. Я там особо ошибки не искал.
Дискретное преобразование Фурье (ДПФ)
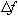 [fmin;fmax]
[fmin;fmax]fo, Гц
M=(целая часть)]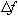 /fo[
/fo[
Тпре=1/fo, сек
fд либо по достаточному условию либо по варианту предложенному выше.
Тд выборок сигнала) N=Тпре/Тд
Рассмотрим аргумент под sin или cos зависящий от времени:
2*
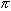 *k*fo*t = 2*
*k*fo*t = 2*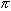 *k*t/Тпре
*k*t/Тпре
Время у нас изменяется дискретно:
t(n)=Tд*n, n=0,1, ... , N-1.
Подставив дискретное время в аргумент, получим аргумент sin и cos зависящий от номера отсчета:
2*
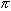 *k*Tд*n/Тпре=2*
*k*Tд*n/Тпре=2*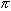 *k*n/N
*k*n/N
здесь n -номер отсчета, k -номер гармоники, N - всего отсчетов.
Умножая синус или косинус с таким аргументом на значение U(t(n)), снятое с АЦП, получим синусоидальную или косинусоидальную составляющую.
Интересно отметить, что вычисление прямо зависит только от N1 и от данных U(t(n)), ну а N зависит от всего остального. Получение N и других параметров требует представления о том, как работает преобразование Фурье, сам же рассчет - это чистая вычислительная математика.
|
Таким образом, задачу вычисления параметров входного сигнала можно разделить на две части:
N и других параметров из свойств сигнала и ДПФ.
fft({Xn},N), с параметрами {Хn} - выборки U(t) в N точках, N - число точек.
Дискретное преобразование Фурье (ДПФ)
Для детектирования "в лоб" только одной составляющей в лучшем случае требуется N операций умножения/сложения. Для М составляющих М*N таких операций.
Сам по себе, рассчет ДПФ уже не имеет прямого отношения самому методу Фурье получения параметров сигнала. Видимо, существует много задач, которые можно свести к системе уравнений такого вида.
Коэффициенты вида sin(2*
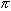 *n*k/N)
*n*k/N)
0, 1, -1
n и k
Если разгруппировать вычисления так, что
-1, +1 заменять вычитанием и сложением
то можно добиться определенного ускорения. Есть так же и аппаратно-зависимые способы, причем убыстрение для одного процессора даст замедление для другого:
Конкретный алгоритм для вашей машины и условий вычисления стоит подобрать самим. ДПФ известно уже много лет, наработано достаточно много готовых решений для многих применений, ими можно воспользоваться, но можно, конечно, самому детально разбирать эти алгоритмы.
Дискретное преобразование Фурье (ДПФ)
Пусть {Un} - набор отсчетов.
Для синусоидальной составляющей с начальной фазой 0
](img8/r1.jpg) ,
, 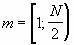
Для косинусоидальной составляющей с начальной фазой 0
](img8/r3.jpg) ,
, 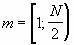
Для постоянной составляющей
](img8/r4.jpg)
Для гармоники m с фазой: амплитуда и фаза
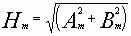 ,
, 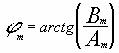
Здесь Аm, Bm - коэффициенты Фурье, или амплитуды sin и cos составляющих с фазой ноль, m - номер детектируемой гармоники.
Можно сгруппировать вместе оценочные утверждения для ДПФ
fo и тем больше время преобразования Тпре, на котором сигнал должен быть стационарным, подходящим для преобразования.
fд определяется в б"ольшей степени шириной полосы входного сигнала 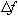
fmax.
N определяется соотношением Tпре и Тд.
Желающие почитать о практических приемах убыстрения ДПФ что-то еще, могут посмотреть, в частности, на этот сайт О БПФ и некоторых его применениях. (Дипломная работа. Корман М. В.).
Кто-то может усомнится в том, что это все работает. Ну, иногда это действительно работает. Вот архив из исходников скачать(download) и откомпилированных программ под ДОС, который просто позволит посмотреть на собственноручно задаваемые сигналы и попреобразовывать туда и обратно с разными параметрами.
Я уже говорил, что важно не потерять все изменения сигнала, например, резкие изменения напряжения, т.е. сохранить форму сигнала. Насколько они резкие и как их не потерять.
Фронтам, резким изменениям, соответствуют высокочастотные составляющие. Если у нас есть физические ограничения полосы входного сигнала, например, идеальный фильтр перед входом, который пропускает сигналы в полосе [0;20] KГц и совсем не пропускает никакие другие частоты, то к нам не может попасть сигнал с такими фронтами, который содержал бы составляющие с частотами выше 20 КГц, поэтому надо отобразить весь диапазон частот после фильтра и мы ничего не потеряем.
Разрешение экрана и то, как мы рисуем сигнал (линиями, точками, сплайнами), тоже определяют качество. Можно хорошо снять и приготовить для рисования сигнал, а потом точками отобразить его в окне размером 8х8 пикселей.
Мы рассмотрели ДПФ как метод для получения информации о сигнале. Но не всегда нужно или можно вычислять преобразование. Если не нужно анализировать сигнал, то можно рисовать его по точкам соединяя кривыми, прямыми или не соединяя. Достаточное количество точек и отличия изображаемого сигнала от оригинала в этом случае определяется не как в ДПФ.
Можно не рассматривать эти достаточные условия, а просто создать драйвер и соответствующие методы отображения для рисования сигнала без ДПФ, снимая данные с максимальной fд. Здесь рисование и выборку можно совместить: сразу рисовать в активный и невидимый буфер по заданным коэффициентам через равные Тд, а, тем временем, будет отображаться другой буфер и надо неспешно ждать готовности нового. Можно применить даже не два, а три буфера, что при несовпадении периода развертки осциллографа Тотобр и периода кадровой синхронизации монитора Ткс позволит применить схему (очистил - повторял_до_готовности - переключился_в_след) без риска отображать разные части сигнала с разной интенсивностью.
Рассмотрим вариант, когда мы имеем за один период кадровой развертки монитора Ткс несколько периодов развертки на экране осциллографа Тотобр. Мы не можем иметь только массив из значений амплитуд точек на периоде Тотобр и складывать арифметически их на каждом периоде, так как получим среднее значение за несколько периодов, вместо нескольких наложенных сигналов. Рисование сразу в буфер, который затем масштабируется в выходной (например, с коэффициентом 1) снимает эту проблему. Эта независимость периодов и отсутствие громоздких вычислений привлекательно в этом методе.
А ДПФ привлекательно тем, что на период самой высокой составляющей в 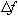
fд, можно сместить акцент на вычисления вместо скорости выборки. После ДПФ с сигналом легко проводить различные преобразования. Сигнал так же можно качественно, красиво и точно, нарисовать для большого количества случаев, как сумму значений синусоид и косинусоид во всех x точках экрана, соединенных, может быть, линиями. Качество сигнала будет пропорционально вычислительной мощности процессора и быстроты алгоритма БПФ.
Оплата же за это - большое количество вычислений. Другая неприятность - некратность Тотобр и Ткс. Куда девать сигнал после каждого периода Тотобр? Очевидное решение - складывать в буфер fifo в памяти. При этом, в среднем, выборки, которые были получены за некоторое время Ттест, должны успевать быть отображены, иначе память под очередь закончится, либо после периода Ттест fifo очищается и периоды сигнала, которые не успели отобразиться, будут утеряны (посылается соответствующее сообщение в окно или считается среднее время потери сигнала). При ДПФ одна часть программы стабильно по Тд в реальном времени быстро снимает отсчеты и бросает их в fifo, другая в обычном режиме, забирая почти все время процессора, преобразует их в коэффициенты Фурье и отображает по заданным параметрам и режиму на экране.
Мы всегда считали, что наш сигнал подходит для ДПФ, но, на практике, возникают сразу несколько вопросов, среди них: представимы ли наши сигналы в виде преобразования Фурье и из каких соображений определить fo. Рассматривая сам метод ДПФ, я везде избегал ответов на них.
При крупном fo сигнал после преобразования и обратного преобразования будет отличаться от оригинала, но, из-за ограниченности вычислительных ресурсов, нам выгодно взять fo как можно большим при сохранении отсутствия искажений. Имея задачу в виде создания программы, мы пока не будем углубляться в детали и искать наиболее оптимальные условия вычислений, а предположим, что сигналы представимы и чем меньше fo, тем лучше.
Для тех, кто смутно представляет как заставить работать програму в реальном времени, программировать таймер и пр. и одновременно смутно представляет себе ДПФ может, для начала, в качестве изучения ДПФ просто считывать с готового PCM(WAV, например) файла в обычной программе и отображать каждый Тотобр по нажатию кнопки.
На этом постановку задачи и рассмотрение трудных и специфичных именно для задачи OSC моментов можно пока закончить. Далее идут вопросы ООП: как и почему сформировать классы (вообще-то этот сайт об ООП). По мере сил и возможностей текст будет этим дополнен, хотя, самостоятельное их получение задача тоже полезная.